General orthonormal curvelinear coordinates (u, v, w) can be obtained from cartesian coordinates by the transformation →x = →x(u, v, w). The unit vectors are then given by: →eu = 1 h1 ∂→x ∂u , →ev = 1 h2∂→x ∂v , →ew = 1 h3 ∂→x ∂w where the factors hi set the norm to 1. Then holds: gradf = 1 h1 ∂f ∂u→eu + 1 h2.. By itself the del operator is meaningless, but when it premultiplies a scalar function, the gradient operation is defined. We will soon see that the dot and cross products between the del operator and a vector also define useful operations. With these definitions, the change in f of (3) can be written as. df = ∇f ⋅ dl = | ∇f | dlcosθ.

All you need to know about Spherical Coordinate System YouTube

The Del Operator in spherical coordinates Lecture 34 Vector Calculus for Engineers YouTube

PPT 8.1 Spherical Coordinates 8.2 Schrödinger's Equation in Spherical Coordinate PowerPoint

PPT PhysicsII 10B11PH211 Theory Thermodynamics Solid State Physics PowerPoint

PPT EE2030 (I) PowerPoint Presentation, free download ID3898424
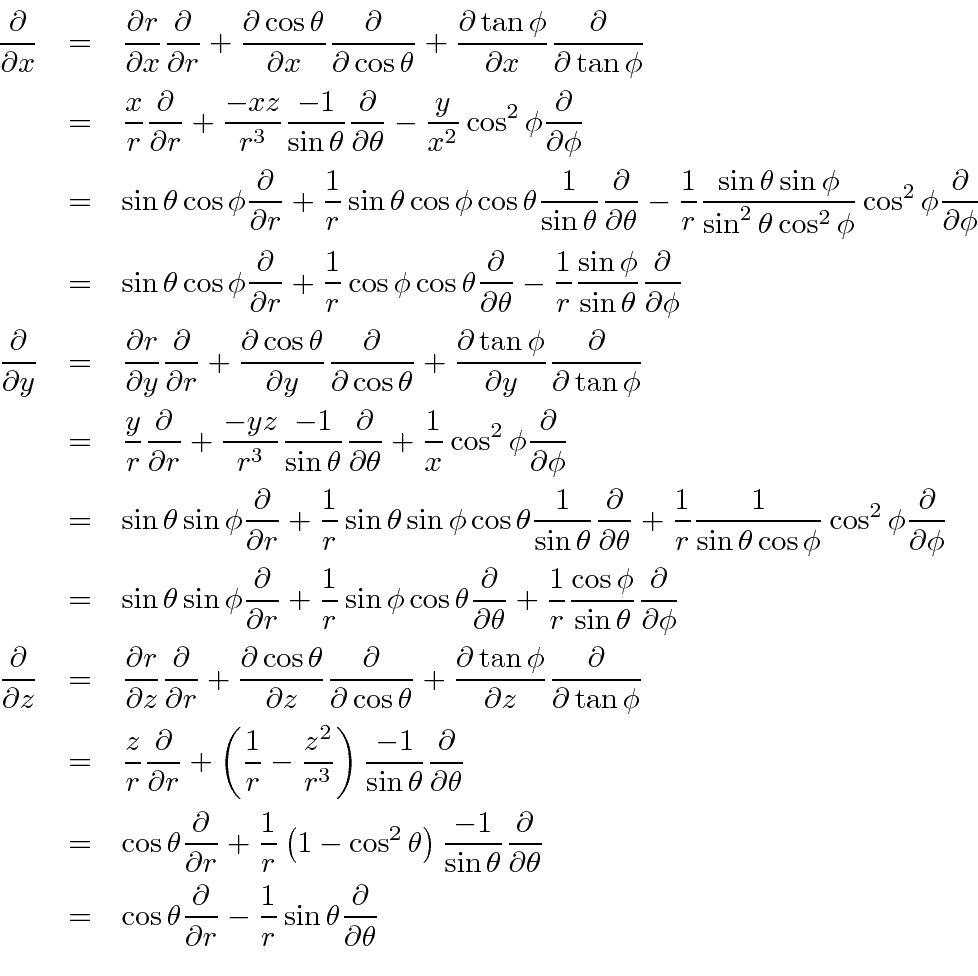
Spherical Coordinates and the Angular Momentum Operators

Multivariable Calculus Unit 5 Lecture 5 Examples with spherical coordinates YouTube

How to remember Del operator in Spherical & cylindrical coordinate POTENTIAL G YouTube
Spherical coordinates Math Insight

Angular momentum operators in Spherical Coordinates Lx in Spherical Ccordinates YouTube

GeeklyHub Spherical Coordinates Transformation Of Coordinates YouTube

Spherical Coordinates Definition, Conversions, Examples

Chapter 01d Spherical Coordinates YouTube

D Spherical Coordinates Chemistry LibreTexts
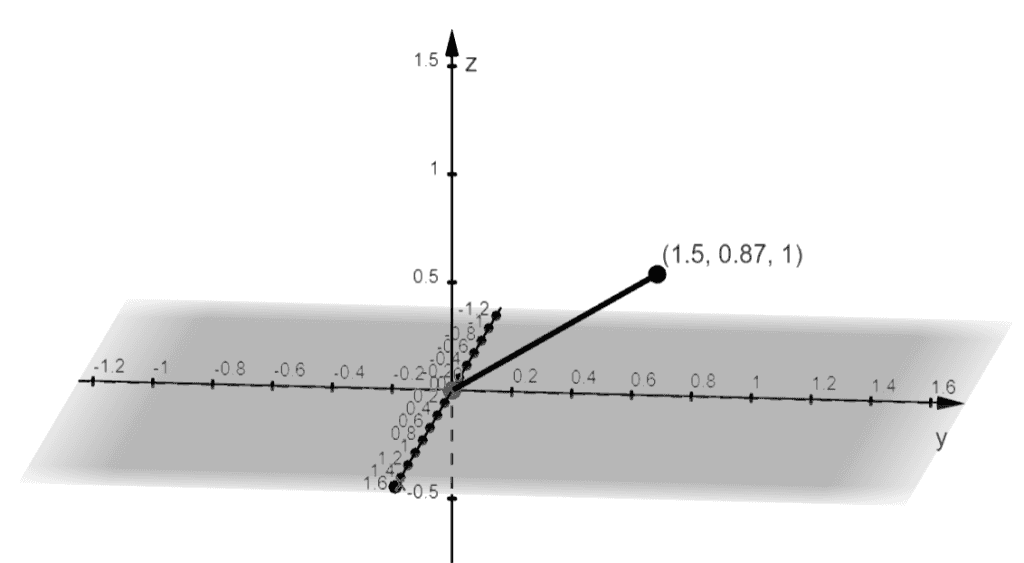
Spherical Coordinates Definition, Graph, and Examples

Del in Cylindrical and Spherical Coordinates Multivariable Calculus Coordinate System
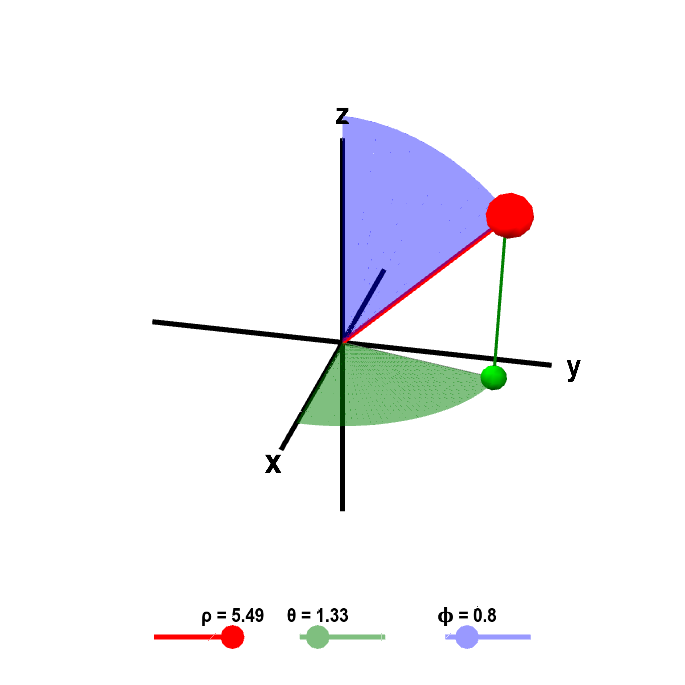
Spherical coordinates Math Insight

Rotation Matrices Derivation of Spherical Coordinates via Multiple Rotations YouTube

Spherical coordinate integration of object bounded by sphere and cone YouTube

Solved Consider Spherical coordinates as illustrated below
The result of cross-multiplying A by the del operator, defined by (2.1.6), is the curl operator. This is the reason for the alternate notation for the curl operator. Thus, in Cartesian coordinates The problems give the opportunity to derive expressions having similar forms in cylindrical and spherical coordinates. The results are summarized in.. Del in cylindrical and spherical coordinates Table with the del operator in cylindrical and spherical coordinates Operaion Cartesian coordinates (x,y,z) Cylindrical coordinates (ρ,φ,z) Spherical coordinates (r,θ,φ) Definition of coordinates x = ρcosφ y = ρsinφ z = z x = rsinθcosφ y = rsinθsinφ z = rcosθ ρ = p x2 +y2